Noch nie hat eine Religion, weder mittelbar noch unmittelbar, weder als Dogma noch als Gleichnis, eine Wahrheit enthalten.

Willkommen auf meiner Netzseite

Wer auf diesen Seiten tiefschürfende Erkenntnisse, Weltverbesserungsvorschläge oder doch wieder nur Bilder siebenachtelnackter Kopulationszielpersonen sucht, der wird leider enttäuscht werden. Meine Seite ist momentan nur dazu da, mir einen Teil meiner Verweisliste virtuell hinterherzutragen. Nein, nicht wie Mutti früher die Stullenbüchse in die Schule zur Freude der gesamten Klasse, sondern viel cooler (Das sagte man früher so.).
Sollten Sie zufällig ähnliche ~~Männerhobbys~~ sinnvolle Interessen haben, sich zum Beispiel für Geschichte, Rechentechnik, Photographie, lange Sätze oder alte Kraftfahrzeuge interessieren, und hier den ein oder anderen Verweis finden, der dazu führt, daß Sie den Abend vor dem Rechner und nicht mit Ihrer besseren Hälfte verbringen, so tut es mir Leid. Natürlich war das alles überhaupt nicht so gewollt.

Universelle Turing-Maschinen

Einleitung

Die Geschichte der universellen Turing-Maschine beginnt im Jahre 1900, als David Hilbert in Paris seine 23 mathematischen Probleme vortrug [Hil00]. Diese Liste umfaßte die wichtigsten offenen Fragen der Mathematik dieser Zeit und war später die Grundlage des sogenannten "Hilbertprogramms", der Suche nach einem vollständigen und widerspruchsfreien Axiomensystem, als Basis für Mathematik und Logik, um sämtliche mathematischen Sätze beweisen zu können. Zusammen mit Wilhelm Ackermann veröffentlichte Hilbert 1928 das Entscheidungsproblem [Hil28], also die Frage, ob es einen Algorithmus gibt, der in einer endlichen Anzahl von Schritten den Wahrheitsgehalt einer FOL-Formel bestimmen kann.

1930/31 erschütterte Kurt Gödel [Goe31; Prop. 8, 11] mit seinem Unvollständigkeitssatz die Mathematiker um Hilbert. Er zeigte nämlich, daß jedes hinreichend mächtige formale System entweder widersprüchlich oder unvollständig und damit auch das hohe gesteckte Ziel des Hilbertprogramms nicht erreichbar ist. Dies führte dazu, daß das Entscheidungsproblem das Interesse vieler Mathematiker weckte, die sich dem Problem auf verschiedenen Wegen näherten.

Kurz nach Alonzo Church [Chu36] zeigte auch Alan Mathison Turing [Tur36], daß das Entscheidungsproblem keine Lösung haben kann. Turing ging dabei einen recht ungewöhnlichen Weg. Er näherte seine Betrachtungen der mechanischen Abarbeitung einer Maschine an und führte das Entscheidungsproblem auf das Halteproblem zurück: "Sei M eine Rechenmaschine (computing machine) und S eine Folge des Eingabealphabets. Gibt es eine Rechenmaschine, die entscheiden kann, ob M mit der Eingabe S hält?". Über einen Widerspruchsbeweis zeigte er dann die Unentscheidbarkeit dieses Problems. Turings "computing machines" gingen später als "Turing-Maschinen" in die Mathematikgeschichte ein.

Ich möchte hier drei universelle Maschinen vorstellen, die nicht nur einfache Berechnungen durchführen, sondern beliebige Programme (Konfigurationen von Turing-Maschinen) und Eingaben einlesen können und daraufhin die Programmausgabe bzw. das Ergebnis berechnen. Turing selbst beschrieb in seiner Arbeit eine erste solche "universal computing machine".

Weiterführende Verweise

UTM von Hopcroft und Ullman

Das erste Beispiel ist die UTM von Hopcroft&Ullman [HU69] in einer von Mark L. Irons korrigierten Fassung.

Als Beispiel für ein Eingabeprogramm dient jedesmal folgender Automat, wenn auch manchmal in leicht abgewandelter Form, der in einer Zeichenkette aus lauter Einsen jedes zweite Vorkommen durch eine Null ersetzt, bis er auf eine Null trifft:

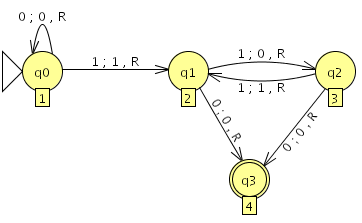Bild 1.1: JFLAP-Darstellung des Basisautomaten

In tabellarischer Schreibweise (neuer Zustand, Kopfbewegung, geschriebenes Zeichen):

Zustand	◊	0	1
q0=1	reject	(1,R,0)	(2,R,1)
q1=2	reject	(4,R,0)	(3,R,0)
q2=3	reject	(4,R,0)	(2,R,1)
q3=4	accept

Kodierung als Eingabe für die UTM

Die Kodierung für die UTM erfolgt über folgende Regeln:

Die Transitionen des Finalzustandes ("accept") werden mit dem Symbol "0" kodiert.
Die Transition "reject" wird mit dem Symbol "0" kodiert.
Alle anderen Transitionen werden kodiert, indem man den Folgezustand durch die entsprechende Anzahl Einsen ersetzt, ein "R" oder "L" anhängt und mit dem jeweiligen Schreibsymbol endet.
Jede Transition wird durch ein "C" eingeleitet. Transitionen werden von oben nach unten und von links nach rechts gelesen.
Zustände werden von einem "C" eingeleitet.
Dem ersten Zustand wird ein zusätzliches "C" vorangestellt.
Der Datenteil folgt unverzüglich der Maschinendefinition und wird von einem "CCC" eingeleitet. Er besteht aus einer Folge von Nullen und Einsen und wird durch ein "◊" beendet (◊ (Blank) bei JFLAP autom. gegeben.).

Wenn wir die Regeln auf unseren Basisautomaten anwenden, erhalten wir folgende Zeichenkette:

CCC0C1R0C11R1 CC0C1111R0C111R0 CC0C1111R0C11R1 CC0C0C0 CCC 1111110 ◊
|||         | |              | |             | |     |  |  |     | |
+--Zustand 1+ +---Zustand 2--+ +--Zustand 3--+ +-Z 4-+  |  +Daten+ |
|||                                                     |          +- Datenende
||+- Transitionsbeginn                                  +- Trennung zum Datenteil
|+- neuer Zustand
+- erster Zustand

Wir wenden noch zwei Initialisierungsregeln an:

Ersetze das dritte "C" von links durch seine Markierung (="c").
Ersetze das erste Symbol des Datenbereichs durch seine Markierung (M("0")="o", M("1")="i", M("◊")="b").

und vervollständigen damit unsere Eingabe für die universelle Turingmaschine:

CCc0C1R0C11R1CC0C1111R0C111R0CC0C1111R0C11R1CC0C0C0CCCi111110◊

Die UTM

Die Turingmaschine:

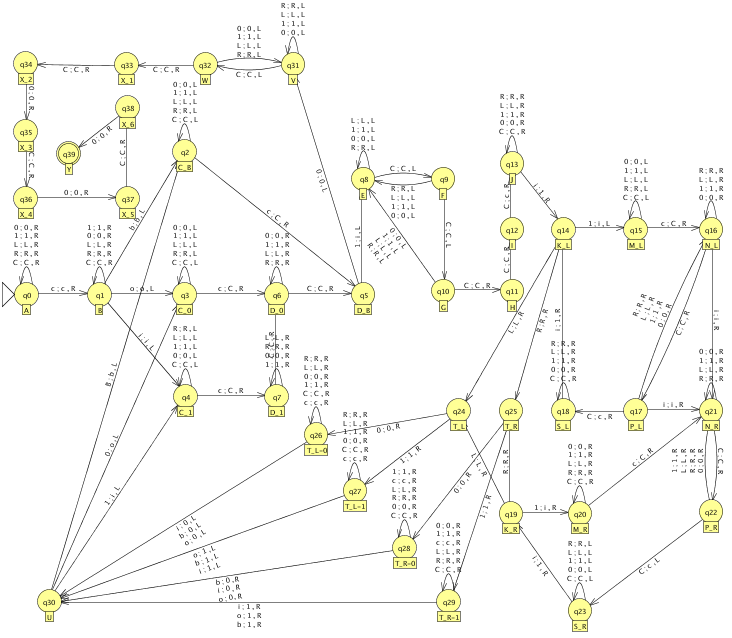Bild 1.2: Die universelle Turingmaschine nach Hopcroft und Ullman

und die zugehörige Transitionstabelle:

Z_org	Z_neu	Eingabebandsymbole
		0	1	C	L	R	b	m₀	m₁	m_C	m_◊
		0	1	C	L	R	◊	o	i	c	b
A	q0	q0,0,R	q0,1,R	q0,C,R	q0,L,R	q0,R,R				q1,c,R
B	q1	q1,0,R	q1,1,R	q1,C,R	q1,L,R	q1,R,R		q3,o,L	q4,i,L		q2,b,L
C_◊	q2	q2,0,L	q2,1,L	q2,C,L	q2,L,L	q2,R,L				q5,C,R
C₀	q3	q3,0,L	q3,1,L	q3,C,L	q3,L,L	q3,R,L				q6,C,R
C₁	q4	q4,0,L	q4,1,L	q4,C,L	q4,L,L	q4,R,L				q7,C,R
D_◊	q5	q31,0,L	q8,i,L
D₀	q6	q6,0,R	q6,1,R	q5,C,R	q6,L,R	q6,R,R
D₁	q7	q7,0,R	q7,1,R	q6,C,R	q7,L,R	q7,R,R
E	q8	q8,0,L	q8,1,L	q9,C,L	q8,L,L	q8,R,L
F	q9	q8,0,L	q8,1,L	q10,C,L	q8,L,L	q8,R,L
G	q10	q8,0,L	q8,1,L	q11,C,R	q8,L,L	q8,R,L
H	q11			q12,C,R
I	q12			q13,c,R
J	q13	q13,0,R	q13,1,R	q13,C,R	q13,L,R	q13,R,R			q14,1,R
K_L	q14		q15,i,L		q24,L,R	q25,R,R
M_L	q15	q15,0,L	q15,1,L	q15,C,L	q15,L,L	q15,R,L				q16,C,R
N_L	q16	q16,0,R	q16,1,R	q17,C,R	q16,L,R	q16,R,R			q21,i,R
P_L	q17	q16,0,R	q16,1,R	q18,c,R	q16,L,R	q16,R,R			q21,i,R
S_L	q18	q18,0,R	q18,1,R	q18,C,R	q18,L,R	q18,R,R			q14,1,R
K_R	q19		q20,i,R		q24,L,R	q25,R,R
M_R	q20	q20,0,R	q20,1,R	q20,C,R	q20,L,R	q20,R,R				q21,C,R
N_R	q21	q21,0,R	q21,1,R	q22,C,R	q21,L,R	q21,R,R
P_R	q22	q21,0,R	q21,1,R	q23,c,L	q21,L,R	q21,R,R
S_R	q23	q23,0,L	q23,1,L	q23,C,L	q23,L,L	q23,R,L			q19,1,R
T_L	q24	q26,0,R	q27,1,R
T_R	q25	q28,0,R	q29,1,R
T_L-0	q26	q26,0,R	q26,1,R	q26,C,R	q26,L,R	q26,R,R		q30,0,L	q30,0,L	q26,c,R	q30,0,L
T_L-1	q27	q27,0,R	q27,1,R	q27,C,R	q27,L,R	q27,R,R		q30,1,L	q30,1,L	q27,c,R	q30,1,L
T_R-0	q28	q28,0,R	q28,1,R	q28,C,R	q28,L,R	q28,R,R		q30,0,R	q30,0,R	q28,c,R	q30,0,R
T_R-1	q29	q29,0,R	q29,1,R	q29,C,R	q29,L,R	q29,R,R		q30,1,R	q30,1,R	q29,c,R	q30,1,R
U	q30	q3,o,L	q4,i,L				q2,b,L
V	q31	q31,0,L	q31,1,L	q32,C,L	q31,L,L	q31,R,L
W	q32	q31,0,L	q31,1,L	q33,C,R	q31,L,L	q31,R,L
X₁	q33			q34,C,R
X₂	q34	q35,0,R
X₃	q35			q36,C,R
X₄	q36	q37,0,R
X₅	q37			q38,C,R
X₆	q38	q39,0,R
Y	q39

Die Abarbeitung der Eingabe

Wenden wir die UTM auf unsere Zeichenkette an, kann man die Arbeitsweise anhand der Kopfposition (rot) nachvollziehen. Die UTM terminiert mit dem korrekten Ergebnis (blau).

Die zugehörige JFLAP-Datei.

UTM von Roger Penrose

Die zweite UTM ist dem Buch von Roger Penrose [Pen91] entnommen. Die Grundidee hierbei ist, daß jeder Turing-Maschine eine sogenannte Turingzahl zugeordnet werden kann.

Als Beispiel dient wieder unser Automat, der in einer Zeichenkette aus lauter Einsen jedes zweite Vorkommen durch eine Null ersetzt, bis er auf eine Null trifft:

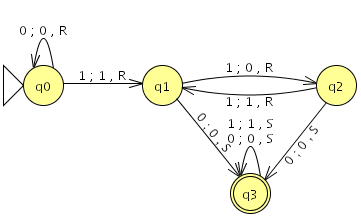Bild 2.1: JFLAP-Darstellung des Basisautomaten

Kodierung als Eingabe für die UTM

Die zugehörigen Transitionen mit den Zustandsnummern in Binärdarstellung:
(Zustandsnummer₍₂₎)(gelesenes Zeichen) → (Zustandsnummer₍₂₎)(geschriebenes Zeichen)(Kopfbewegung)

00	→	00R
01	→	11R
10	→	110S
11	→	100R
100	→	110S
101	→	11R
110	→	110S
111	→	111S

Die fortlaufende Numerierung auf der linken Seite kann weggelassen werden. Die rechte Seite ergibt von oben nach unten folgende Zeichenkette:

00R11R110S100R110S11R110S111S

Jedes 00 kann weggelassen werden, 01 wird als 1 kodiert. Weiterhin gelten folgende Darstellungen:

0	für 0 oder 0
10	für 1 oder 1
110	für R
1110	für L
11110	für S

Wir erhalten das Zwischenergebnis:

110 1010 110 10100 11110 1000 110 10100 11110 1010 110 10100 11110 101010 11110

Ebenso wird angenommen, daß die Transition 00 → 00R jedem Automaten immanent ist (0 fungiert hier ebenso als Blank; also gehe bis zum Wortanfang). Da jede Transition mit R, L oder S aufhört, kann die Folge "110" am Anfang und am Ende gestrichen werden. Die resultierende Zeichkette stellt dann die Turingzahl in Binärdarstellung dar:

m = 10101101010011110100011010100111101010110101001111010101011

Bzw. in Dezimaldarstellung: m = 390258686802173611.

Die UTM

Eine solche Turingmaschine T_m angewandt auf eine Zahl n ergibt eine Zahl p: T_m(n)=p. Eine universelle Turingmaschine U nimmt als Eingaben die Zahlen m, n und berechnet daraus p: U(m,n)=p. Penrose gibt folgende universelle Turingmaschine an:

U = 724485533533931757719839503961571123795236067255655963110814479
6606505059404241090310483613632359365644443458382226883278767626556
1446928141177150178425517075540856576897533463569424784885970469347
2573998858228382779529468346052106116983594593879188554632644092552
5505820555989451890716537414896033096753020431553625034984529832320
6515830476641421307088193297172341510569802627346864299218381721573
3348282307345371342147505974034518437235959309064002432107734217885
1492760797597634415123079586396354492269159479654614711345700145048
1673375621725734645227310544829807849651269887889645697609066342044
7798902191443793283001949357096392170390483327088259620130177372720
2718625919914428275437422351355675134084222299889374410534305471044
3686958764051781280194375308138706399427728231564252892375145654438
9905278079324114482614235728619311833261065612275553181020751108533
7633806031082361675045635852164214869542347187426437544428790062485
8270912404220765387542644541334517485662915742999095026230097337381
3772416217274772361020678685400289356608569682262014198248621698902
6091309402985706001743006700868967590344734174127874255812015493663
9389969058177385916540553567040928213322216314109787108145997866959
9704509681841906299443656015145490488092208448003482249207730403043
1884298993931352668823496621019471619107014619685231928474820344958
9770955356110702758174873332729667899879847328409819076485127263100
1740166787363477605857245036964434897992034489997455662402937487668
8397514044516657077500605138839916688140725455446652220507242623923
7921152531816251253630509317286314220040645713052758023076651833519
95689139748137504926429605010013651980186945639498

Die Dekodierung führt zu folgender Transitionstabelle¹:

Als Trennung zwischen eingegebener Turingmaschinenzahl m und dem Argument n dient die Folge "111110", außerdem wird von ungeraden n die letzte "1" gestrichen und jedes n mit "1" abgeschlossen. Wir erhalten für n=1111110 die UTM-Eingabe:

10101101010011110100011010100111101010110101001111010101011 111110 1111110 1²

¹ Die Transitionstabelle für JFLAP wurde um einen Zustand "201" erweitert, der den Endzustand darstellt, da JFLAP mit finalem 0-Zustand keinen Schritt auf dem Band macht.

² JFLAP muss links und rechts genügend "Reservenullen" als Eingabe erhalten, da die Null ebenfalls als Blank fungiert. Benutzen Sie daher die erste Zeile der Ausgabe als Eingabe.

Die Abarbeitung der Eingabe

Auch bei dieser Abarbeitung ist die Kopfposition der TM wieder rot und das Ergebnis blau dargestellt.

Die zugehörige JFLAP-Datei.

UTM von Marvin Minsky

Die beiden letzten UTMs zeichneten sich entweder durch ein großes Arbeitsalphabet oder durch eine große Anzahl von Zuständen aus. Marvin Minsky suchte Anfang der 60er Jahre eine Möglichkeit, eine universelle Turingmaschine mit kleinem Eingabealphabet und niedriger Zustandszahl zu konstruieren. 1962 veröffentlichte er seine Lösung ([Min62], auch beschrieben in [Min67]), eine (7,4)-UTM mit sieben Zuständen und vier Symbolen. In den vergangenen Jahren folgten weitere Veröffentlichungen, ua. von Rogozhin (zB. [Rog96]) mit (2,24), (3,10), (4,7), (5,5), (6,4), (10,3) und (18,2) oder Baiocchi (zB. [Bai01]) mit (7,4), (10,3) und (19,2)-Varianten.

Aktualisierung: Im Herbst 2007 ist es Alex Smith gelungen [Smi07], den Nachweis zu führen, daß eine von Stephen Wolfram gefundene Turingmaschine mit nur drei Farben und zwei Zuständen universell ist.

Die gemeinsame Grundidee dieser Maschinen sind die sogen. Tag-Systeme. Ein Tag-System besteht aus einer Menge A = {a₁,a₂...a_n} von Zeichen, dem Alphabet, und einer Menge W von Wörtern über A. Für jedes 1 ≤ i ≤ n gibt es ein solches Wort W_i ∈ W, sofern es kein Haltesymbol ist. Weiterhin ist zu jedem Tag-System eine Eliminierungszahl P festgelegt.

Beispiel

Gegeben sei ein Tag-System mit P=2 und den Produktionen a_i → W_i:

a₁	→	a₃a₃a₃
a₂	→	a₃
a₃	→	halt

Bei der Abarbeitung eines Startwortes s = a_ia_jW werden die ersten P Zeichen gelöscht und an das Wortende die rechte Seite der Produktion von a_i → W_i angehangen: s' = WW_i für P=2. Dies wird wiederholt, bis das erste Zeichen ein Haltesymbol ist. Bei einem Startwort a₁a₂a₂ ergibt das für unser Beispiel: a₁a₂a₂ → a₂a₃a₃a₃ → a₃a₃a₃.

Turing-Maschine → Tag-System

Cocke und Minsky wiesen 1964 [CoMi64] die Universalität von Tag-Systemen mit P=2 nach. Wir werden uns daher auf P=2 beschränken und uns weiterhin an einer leicht abgewandelten Form von Minskys UTM halten, die Raphael M. Robinson in [Rob91] beschrieben hat. Ebenfalls in dieser Arbeit ist ein Algorithmus zur Reduzierung einer n-Symbol-TM zu einer 2-Symbol-TM enthalten. Für unseren Beispielautomaten, der wieder jede zweite "1" in eine "0" umwandelt, bis er auf eine Null trifft, ist dies aber nicht notwendig.

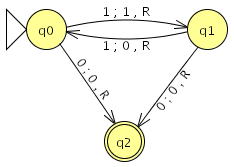Bild 3.1: JFLAP-Darstellung des Basisautomaten

Wie funktioniert nun die Umwandlung unserer Turingmaschine in ein Tag-System? Zuerst benötigen wir eine Darstellung des Arbeitsbandes. Wir nehmen dazu an, der Kopf der Turingmaschine befindet sich über c₀ und die linke und rechte Seite des Bandes stellen nat. Zahlen in Binärdarstellung dar:

   <---m---  --n-->
... c_-3c_-2c_-1c₀c₁c₂c₃ ...

mit

j	=	c₀
m	=	c_-1 + 2c_-2 + 4c_-3 + 8c_{-4 + ...}
n	=	c₁ + 2c₂ + 4c₃ + 8c₄ + ...

Von der üblichen Quintupeldarstellung für Transitionen ausgehend (q_i,s_j,s_k,D,q_l) = (Ist-Zustand, gelesenes Zeichen, geschriebenes Zeichen, Kopfbewegung, Nachfolgezustand), können wir den Zustand unserer Turingmaschine jetzt als Quadrupel (i,j,m,n) beschreiben. Für unser Band wählen wir deshalb die Darstellung:

A_ijA_ij(a_ija_ij)^mB_ijB_ij(b_ijb_ij)ⁿ

Um unsere Transitionen (q_i,s_j,s_k,D,q_l) in Produktionen umzuwandeln benutzen wir folgende Regeln:

1. Produktionen für (q_i,s_j,s_k,R,q_l)

A_ij	→	C_ijC_ij(c_ijc_ij)^k
a_ij	→	(c_ijc_ij)²
B_ij	→	D_ij
b_ij	→	d_ij

2. Produktionen für (q_i,s_j,s_k,L,q_l)

A_ij	→	C_ij
a_ij	→	c_ij
B_ij	→	D_ijD_ij(d_ijd_ij)^k
b_ij	→	(d_ijd_ij)²

3. Produktionen für beide Varianten

C_ij	→	E_l1E_l0
c_ij	→	e_l1e_l0
D_ij	→	F_l1F_l0
d_ij	→	f_l1f_l0

4. Produktionen unabhängig von der Transition

E_i0	→	A_i0A_i0A_i0
E_i1	→	A_i1A_i1
e_ij	→	a_ija_ij
F_ij	→	B_ijB_ij
f_ij	→	b_ijb_ij

Besitzt ein Zustand keine wegführenden Transitionen (im Beispiel q₂), können wir die entspr. C_ij, c_ij, D_ij und d_ij aus unserem Alphabet streichen. Des Weiteren verlieren die jeweiligen A_ij, a_ij und b_ij ihre Indizes, so daß A unser einziges Haltesymbol ist (a, b und B_ij sind "virtuelle Haltesymbole").

Wenden wir die Regeln auf unseren Basisautomaten an, erhalten wir folgende Produktionen (A₂₀ = A₂₁ = A, a₂₀ = a₂₁ = a, b₂₀ = b₂₁ = b, doppelte Produktionen wurden weggelassen):

A	→	halt
A₀₀	→	C₀₀C₀₀
a₀₀	→	c₀₀c₀₀c₀₀c₀₀
B₀₀	→	D₀₀
b₀₀	→	d₀₀
C₀₀	→	E₂₁E₂₀
c₀₀	→	e₂₁e₂₀
D₀₀	→	F₂₁F₂₀
d₀₀	→	f₂₁f₂₀
E₀₀	→	A₀₀A₀₀A₀₀
E₀₁	→	A₀₁A₀₁
e₀₀	→	a₀₀a₀₀
F₀₀	→	B₀₀B₀₀
f₀₀	→	b₀₀b₀₀
A₀₁	→	C₀₁C₀₁c₀₁c₀₁
a₀₁	→	c₀₁c₀₁c₀₁c₀₁
B₀₁	→	D₀₁
b₀₁	→	d₀₁
C₀₁	→	E₁₁E₁₀
c₀₁	→	e₁₁e₁₀
D₀₁	→	F₁₁F₁₀
d₀₁	→	f₁₁f₁₀
e₀₁	→	a₀₁a₀₁
F₀₁	→	B₀₁B₀₁
f₀₁	→	b₀₁b₀₁
A₁₀	→	C₁₀C₁₀
a₁₀	→	c₁₀c₁₀c₁₀c₁₀
B₁₀	→	D₁₀
b₁₀	→	d₁₀
C₁₀	→	E₂₁E₂₀
c₁₀	→	e₂₁e₂₀
D₁₀	→	F₂₁F₂₀
d₁₀	→	f₂₁f₂₀
E₁₀	→	A₁₀A₁₀A₁₀
E₁₁	→	A₁₁A₁₁
e₁₀	→	a₁₀a₁₀
F₁₀	→	B₁₀B₁₀
f₁₀	→	b₁₀b₁₀
A₁₁	→	C₁₁C₁₁
a₁₁	→	c₁₁c₁₁c₁₁c₁₁
B₁₁	→	D₁₁
b₁₁	→	d₁₁
C₁₁	→	E₀₁E₀₀
c₁₁	→	e₀₁e₀₀
D₁₁	→	F₀₁F₀₀
d₁₁	→	f₀₁f₀₀
e₁₁	→	a₁₁a₁₁
F₁₁	→	B₁₁B₁₁
f₁₁	→	b₁₁b₁₁
E₂₀	→	AAA
E₂₁	→	AA
e₂₀	→	aa
F₂₀	→	B₂₀B₂₀
f₂₀	→	bb
e₂₁	→	aa
F₂₁	→	B₂₁B₂₁
f₂₁	→	bb
B₂₀	→	halt
B₂₁	→	halt
a	→	halt
b	→	halt

Die Abarbeitung des Tag-Systems

Wir überprüfen die Abarbeitung des Tag-Systems. Als Startkonfiguration wählen wir die Zeichenkette "1111", der Automat befindet sich im Zustand q₀ und liest die erste "1". Alle anderen Felder des Eingabebandes sind mit "0" belegt. In unserer Tag-Darstellung mit der beschriebenen TM-Abstraktion erhalten wir das Wort:

<---m--- ---n--->
... 000011110000 ...

A₀₁A₀₁B₀₁B₀₁(b₀₁b₀₁)⁷

Wir dekodieren das Ergebnis:

AAaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaB₂₀B₂₀ = A₂₀A₂₀(a₂₀a₂₀)²⁰B₂₀B₂₀
m = 20 = 10100₍₂₎

halten also im Zustand 2, über einer Null, mit dem Ergebnis: "10100". Unser Tag-System verhält sich also genau wie unser Basisautomat.

Kodierung als Eingabe für die UTM

Um unser Tag-System als Eingabe für die UTM aufzubereiten, gehen wir von einem Alphabet a₀, a₁, a₂ ... a_p mit den zugehörigen Produktionen a_i → a_i1a_i2 ... a_{in_i} aus¹.

Für jedes 0 ≤ i ≤ p definieren wir ein N_i mit:

N_i = (n₀ + 1) + (n₁ + 1) + ... + (n_i-1 + 1)

wobei n_i = 0, falls a_i ein Haltesymbol ist.

N₀ = 0, N₁ = 1

Die rechte Seite einer Produktion wird mit Hilfe der eben berechneten N_i kodiert:

P_i = 1 0^N_{in_i} 01 ... 01 0^N_i2 01 0^N_i1 01

und kann zusammen mit den anderen Produktionen auf dem Eingabeband dargestellt werden²:

... 0 0 1 P_m ... P₂ P₁ 1 0 ... 0 S 0 0 ...

Uns fehlt nur noch die Kodierung des Startwortes S = a_ra_s ... a_z:

S = 2^N_r 3 2^N_s 3 ... 3 2^N_z

Beachten Sie, daß a₀, das Haltesymbol, als leere Zeichenkette kodiert wird. Ein Tag-Wort a₀a₀a₁a₁ würde also als "33232" dargestellt werden.

Für unser Beispiel und folgender Numerierung ergeben sich dann die n_i, N_i und P_i:

i	a_i	n_i	N_i	P_i
0	A	0	0	-
1	A₀₀	2	1	1 0¹³ 01 0¹³ 01
2	a₀₀	4	4	1 0¹⁶ 01 0¹⁶ 01 0¹⁶ 01 0¹⁶ 01
3	B₀₀	1	9	1 0¹⁹ 01
4	b₀₀	1	11	1 0²² 01
5	C₀₀	2	13	1 0¹⁴⁹ 01 0¹⁵³ 01
6	c₀₀	2	16	1 0¹⁵⁶ 01 0¹⁶⁵ 01
7	D₀₀	2	19	1 0¹⁵⁹ 01 0¹⁶⁸ 01
8	d₀₀	2	22	1 0¹⁶² 01 0¹⁷¹ 01
9	E₀₀	3	25	1 0¹ 01 0¹ 01 0¹ 01
10	E₀₁	2	29	1 0⁴¹ 01 0⁴¹ 01
11	e₀₀	2	32	1 0⁴ 01 0⁴ 01
12	F₀₀	2	35	1 0⁹ 01 0⁹ 01
13	f₀₀	2	38	1 0¹¹ 01 0¹¹ 01
14	A₀₁	4	41	1 0⁵⁸ 01 0⁵⁸ 01 0⁵⁵ 01 0⁵⁵ 01
15	a₀₁	4	46	1 0⁵⁸ 01 0⁵⁸ 01 0⁵⁸ 01 0⁵⁸ 01
16	B₀₁	1	51	1 0⁶¹ 01
17	b₀₁	1	53	1 0⁶⁴ 01
18	C₀₁	2	55	1 0¹⁰⁰ 01 0¹⁰⁴ 01
19	c₀₁	2	58	1 0¹⁰⁷ 01 0¹⁴⁰ 01
20	D₀₁	2	61	1 0¹¹⁰ 01 0¹⁴³ 01
21	d₀₁	2	64	1 0¹¹³ 01 0¹⁴⁶ 01
22	e₀₁	2	67	1 0⁴⁶ 01 0⁴⁶ 01
23	F₀₁	2	70	1 0⁵¹ 01 0⁵¹ 01
24	f₀₁	2	73	1 0⁵³ 01 0⁵³ 01
25	A₁₀	2	76	1 0⁸⁸ 01 0⁸⁸ 01
26	a₁₀	4	79	1 0⁹¹ 01 0⁹¹ 01 0⁹¹ 01 0⁹¹ 01
27	B₁₀	1	84	1 0⁹⁴ 01
28	b₁₀	1	86	1 0⁹⁷ 01
29	C₁₀	2	88	1 0¹⁴⁹ 01 0¹⁵³ 01
30	c₁₀	2	91	1 0¹⁵⁶ 01 0¹⁶⁵ 01
31	D₁₀	2	94	1 0¹⁵⁹ 01 0¹⁶⁸ 01
32	d₁₀	2	97	1 0¹⁶² 01 0¹⁷¹ 01
33	E₁₀	3	100	1 0⁷⁶ 01 0⁷⁶ 01 0⁷⁶ 01
34	E₁₁	2	104	1 0¹¹⁶ 01 0¹¹⁶ 01
35	e₁₀	2	107	1 0⁷⁹ 01 0⁷⁹ 01
36	F₁₀	2	110	1 0⁸⁴ 01 0⁸⁴ 01
37	f₁₀	2	113	1 0⁸⁶ 01 0⁸⁶ 01
38	A₁₁	2	116	1 0¹²⁸ 01 0¹²⁸ 01
39	a₁₁	4	119	1 0¹³¹ 01 0¹³¹ 01 0¹³¹ 01 0¹³¹ 01
40	B₁₁	1	124	1 0¹³⁴ 01
41	b₁₁	1	126	1 0¹³⁷ 01
42	C₁₁	2	128	1 0²⁵ 01 0²⁹ 01
43	c₁₁	2	131	1 0³² 01 0⁶⁷ 01
44	D₁₁	2	134	1 0³⁵ 01 0⁷⁰ 01
45	d₁₁	2	137	1 0³⁸ 01 0⁷³ 01
46	e₁₁	2	140	1 0¹¹⁹ 01 0¹¹⁹ 01
47	F₁₁	2	143	1 0¹²⁴ 01 0¹²⁴ 01
48	f₁₁	2	146	1 0¹²⁶ 01 0¹²⁶ 01
49	E₂₀	3	149	1 0⁰ 01 0⁰ 01 0⁰ 01
50	E₂₁	2	153	1 0⁰ 01 0⁰ 01
51	e₂₀	2	156	1 0¹⁷⁶ 01 0¹⁷⁶ 01
52	F₂₀	2	159	1 0¹⁷⁴ 01 0¹⁷⁴ 01
53	f₂₀	2	162	1 0¹⁷⁷ 01 0¹⁷⁷ 01
54	e₂₁	2	165	1 0¹⁷⁶ 01 0¹⁷⁶ 01
55	F₂₁	2	168	1 0¹⁷⁵ 01 0¹⁷⁵ 01
56	f₂₁	2	171	1 0¹⁷⁷ 01 0¹⁷⁷ 01
57	B₂₀	0	174	101
58	B₂₁	0	175	101
59	a	0	176	101
60	b	0	177	101

und für die oben gewählte Startkonfiguration:

S = 2⁴¹ 3 2⁴¹ 3 2⁵¹ 3 2⁵¹ (3 2⁵³ 3 2⁵³)⁷

¹ Sollte nicht für jedes Symbol eine Produktion vorhanden sein, wird das entsprechende a_i als "virtuelles Haltesymbol" definiert.

² Zwischen den P_i uns S befindet sich mindestens eine Null. Der Exponent n meint immer die n-fache Wiederholung des Basissymbols.

Die UTM

Unsere universelle Turingmaschine besitzt 27 Transitionen. Die Tripel in den Zellen sind (s_k,D,q_l): zB. befinden wir uns im Zustand q₂, lesen eine "0", schreiben eine "2", bewegen den Kopf nach links und gehen in den Zustand q₄ über.

Zustand	0	1	2	3
q₀	(2,R,0)	(3,R,0)	(0,L,1)	(2,L,4)
q₁	(0,L,1)	(3,R,0)	(0,L,1)	(1,L,1)
q₂	(2,L,4)	(3,R,2)	(2,R,2)	(1,R,2)
q₃	(3,L,4)	(3,R,3)	(2,R,3)	(1,R,3)
q₄	-	(3,L,4)	(2,L,4)	(1,L,5)
q₅	(2,R,2)	(1,L,6)	(2,L,5)	(1,L,5)
q₆	(2,R,3)	(1,R,6)	(0,R,6)	(0,R,0)

Die Abarbeitung

Die Abarbeitung beginnt die UTM im Zustand q₀ über dem ersten Zeichen von S. Wir müssen den Automaten daher wieder an JFLAP anpassen und auch die Eingabe wieder mit genügend Reservenullen ("0" dient wieder als Blank) versehen. Wir empfehlen allerdings, in diesem Fall eine selbstgeschriebene kleine Turingmaschine mit geeigneten Datenstrukturen zu verwenden. Dies würde auch die Ergebnisdekodierung vereinfachen.

Leider verbietet sich eine vernünftige Darstellung der Ausgabe. Der geneigte Leser möge sich den Speicherbedarf einer vierfarbigen {0,1,2,3} Grafik mit einer Breite von 41.714 Pixeln (Arbeitsband am Ende der Abarbeitung mit jeweils zwei Blanks links und rechts) und einer Höhe von 1.592.723.815 Pixeln (Anzahl der Iterationen), gegebenfalls mit geeigneter Komprimierung (die UTM hierbei nicht vergessen ;)), überlegen.

Wir beschränken uns daher auf den wesentlichen Teil:

S_erg = 2⁰ 3 2⁰ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁶ 3 2¹⁷⁴ 3 2¹⁷⁴

Ergebnisdekodierung

Leider hat die Maschine einen kleinen Schönheitsfehler. Die erste "3" (blau) wird immer durch eine "2" ersetzt. Vor dem Dekodieren muß man dies erst wieder rückgängig machen. In vereinfachter Schreibweise:

S_erg = 2^N₀ 3 2^N₀ 3 (2^N₁₇₆ 3 2^N₁₇₆ 3)²⁰ 2^N₁₇₄ 3 2^N₁₇₄

und mit Hilfe der obigen Tabelle dekodiert:

S_erg = AA(aa)²⁰B₂₀B₂₀

Wir erhalten also genau das erwartete und oben bereits hergeleitete Ergebnis.

Die zugehörige JFLAP-Datei.

Weiterführende Verweise

Brainfuck: Nachweis der Turing-Vollständigkeit über eine Tag-System-UTM
Wolfram: A New Kind Of Science: Universality in Turing Machines and Other Systems
Marvin Minsky: Netzseite

Literatur

[Bai01]: Baiocchi, Claudio: Three Small Universal Turing Machines, LNCS 2055, 2001.
[Chu36]: Church, Alonzo: An unsolvable problem of elementary number theory. American Journal of Mathematics/58, 1936.
[CoMi64]: Cocke, John; Minsky, Marvin: Universality of Tag Systems With P=2, ACM Vol. 11, 1964.
[Goe31]: Gödel, Kurt: Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I, 1931.
[Hil00]: Hilbert, David: Mathematische Probleme: Vortrag zum Mathematiker-Kongreß zu Paris, 1900. (Netzversion)
[Hil28]: Hilbert, David; Ackerman, Wilhelm: Grundzüge der theoretischen Logik, 1928.
[HU69]: Hopcroft, Ullman: Formal Languages and Their Relation to Automata, 1969.
[Min62]: Minsky, Marvin: Size and structure of universal Turing machines using tag systems, Proceedings of Symposia in Pure Mathematics, Vol. 5, AMS, 1962.
[Min67]: Minsky, Marvin: Computation: Finite And Infinite Machines, Prentice Hall, 1967.
[Pen91]: Penrose, Roger: Computerdenken, Spektrum der Wissenschaft Verlagsgesellschaft, Heidelberg 1991.
[Rob91]: Robinson, Raphael M.: Minsky's Small Universal Turing Machine, IJM Vol. 2 No. 5, 1991.
[Rog96]: Rogozhin, Yurii: Small universal Turing machines, TCS 168, 1996.
[Smi07]: Smith, Alex: Universality of Wolfram's 2, 3 Turing Machine. (Netzversion)
[Tur36]: Turing, Alan Mathison: On Computable Numbers, with an application to the Entscheidungsproblem, 1936. (Netzversion)

Willkommen auf meiner Netzseite

Universelle Turing-Maschinen

Inhalt

Einleitung

Weiterführende Verweise

UTM von Hopcroft und Ullman

Kodierung als Eingabe für die UTM

Die UTM

Die Abarbeitung der Eingabe

UTM von Roger Penrose

Kodierung als Eingabe für die UTM

Die UTM

Die Abarbeitung der Eingabe

UTM von Marvin Minsky

Beispiel

Turing-Maschine → Tag-System

1. Produktionen für (qi,sj,sk,R,ql)

2. Produktionen für (qi,sj,sk,L,ql)

3. Produktionen für beide Varianten

4. Produktionen unabhängig von der Transition

Die Abarbeitung des Tag-Systems

Kodierung als Eingabe für die UTM

Die UTM

Die Abarbeitung

Ergebnisdekodierung

Weiterführende Verweise

Literatur

1. Produktionen für (q_i,s_j,s_k,R,q_l)

2. Produktionen für (q_i,s_j,s_k,L,q_l)